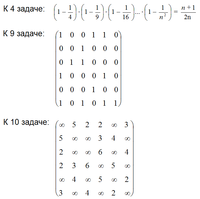
Контрольная работа по дисциплине: Дискретная математика. Вариант №7 (2-й семестр)

Задача 1
Доказать равенства, используя свойства операций над множествами и определения операций. Проиллюстрировать при помощи диаграмм
Эйлера-Венна.
а) (A\C)  (B\C) = (AB)\C
б) (A\B)C=(AC)\(BC)

Задача 2
Даны два конечных множества: А={a,b,c}, B={1,2,3,4}; бинарные отношения P1 AB, P2 B2. Изобразить P1, P2 графически. Найти P = (P2P1)^(–1). Выписать области определения и области значений всех трех отношений: P1, P2, Р. Построить матрицу [P2], проверить с ее помощью, является ли отношение P2 рефлексивным, симметричным, антисимметричным, транзитивным. P1 = {(a,1),(b,3),(b,1),(b,4),(c,3),(c,2)}; P2 = {(1,3),(1,4),(2,2),(3,3),(4,3),(4,4)}.

Задача 3
Задано бинарное отношение P R^2; найти его область определения и область значений. Проверить по определению, является ли P рефлексивным, симметричным, антисимметричным, транзитивным., P = {(x,y) | x^2 + y^2 = 4}.

Задача 4
Доказать утверждение методом математической индукции (см. скрин): для n >= 2.

Задача 5
Восемь студентов должны сдавать зачет по пяти предметам: физике, архитектуре ЭВМ, математическому анализу, английскому языку и истории. Все зачеты назначены на одно время и каждый может сдавать только один зачет, поэтому студентам нужно распределиться на группы.
Сколькими способами это можно сделать?
Сколькими способами они могут разместиться после зачета за двумя совершенно одинаковыми столиками (не менее чем по одному) для того, чтобы отпраздновать результаты?

Задача 6
Сколько существует положительных трехзначных чисел: а) не делящихся ни на одно из чисел 5, 6, 16? б) делящихся ровно на одно из этих трех чисел?

Задача 7
Найти коэффициенты при a=x^4•y•z^3, b=x•y^4•z, c=y^2•z^4 в разложении (3•x^2+5•y+2•z)^6.

Задача 8
Найти последовательность {an}, удовлетворяющую рекуррентному соотношению 3•an+2 – 8•an+1 + 5•an = 0• и начальным условиям a1=10, a2=20.

Задача 9
Орграф задан матрицей смежности (см. скрин). Необходимо:  
а) нарисовать граф;  
б) выделить компоненты сильной связности;  
в) заменить все дуги ребрами и в полученном неориентированном графе найти эйлерову цепь (или цикл).

Задача 10
Взвешенный граф задан матрицей длин дуг (см. скрин). Нарисовать граф. Найти:
а) остовное дерево минимального веса;  
б) кратчайшее расстояние от вершины v3 до остальных вершин графа, используя алгоритм Дейкстры.

Оценка - отлично!
Преподаватель: Бах О.А.