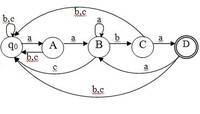
300

Теория языков программирования и методы трансляции. КУРСОВАЯ РАБОТА. Вариант №18

ID: 149642
Дата закачки: 27 Января 2015
Продавец: Shamrock (Напишите, если есть вопросы)
    Посмотреть другие работы этого продавца

Тип работы: Работа Курсовая
Форматы файлов: Исполняемые фалы (EXE), Microsoft Word, Text (Plain), VisualC++
Сдано в учебном заведении: СибГУТИ

Описание:
Написать программу для автоматического построения детерминированного конечного автомата (ДКА) по словесному описанию языка.
Вход программы: алфавит языка, обязательная конечная подцепочка, цепочки для распознавания.
Выход: построенный ДКА (все 5 элементов), результат проверки цепочек.
Подробно:
Язык задан своим алфавитом и обязательной конечной подцепочкой всех цепочек языка. В конечной подцепочке не должно находиться символов, не содержащихся в алфавите. В крайнем случае она может быть и пустой.
Программа должна:
1. по предложенному описанию регулярного языка строить ДКА, распознающий этот язык, в том виде, как он рассматривался в теории, раздел 2.2.2;
2. с помощью построенного ДКА проверять вводимые пользователем цепочки на их принадлежность этому языку.
ДКА должен быть полностью определённым. Функция переходов ДКА может изображаться в виде таблицы или графа, вариант вида её представления выбирается разработчиком.
Наиболее простой способ построения такого ДКА состоит в том, чтобы сначала по описанию языка построить НКА (недетерминированный конечный автомат), а затем преобразовать его согласно рассмотренному в разделе 2.2.2 алгоритму. При выборе такого способа построения ДКА промежуточный результат в виде НКА необходимо также отображать на экране по просьбе пользователя.
По желанию автора допускаются и другие способы построения ДКА.
После построения ДКА пользователь может вводить произвольные цепочки для проверки их на принадлежность исходному языку. Разбор цепочек автоматом следует поэтапно отображать на экране в виде последовательной смены конфигураций в соответствии с лабораторной работой №2.
Рассмотрим пример построения ДКА.
Задан язык: алфавит {0,1,a,b} и обязательная конечная подцепочка «01ab». Анализируем задание: язык будет состоять из цепочек любой длины, заканчивающихся на «01ab», например {1a01ab, bb01ab, ba101ab, …}. Тогда ДКА должен иметь вид M(Q,{a,b,с},d,q0,F), множество состояний Q и заключительные состояния F определятся в процессе построения. Разберёмся с построением функции переходов d. Очевидно, что пустая цепочка в языке не содержится (поскольку есть непустая обязательная конечная цепочка). Сначала определимся с минимальной цепочкой языка – это ‘aaba’, и построим для неё граф переходов.

Если выбрать способ с предварительным построением НКА, то такой автомат выглядит очевидным образом. Сначала могут быть прочитаны любые символы алфавита в любом количестве, а затем конечная подцепочка:
Недетерминированность автомата вызвана тем, что из начального состояния существует два перехода по одному символу алфавита (‘a’). Осталось преобразовать построенный автомат в детерминированный. Для этого построим таблицу переходов:
 вход Исходную таблицу переходов отделим от остальной части жирной линией.
Для упрощения процесса будем создавать не все возможные новые состояния, которые могут получиться в результате сочетаний исходных состояний, а только те, которые реально возникают при построении. Сначала это единственное состояние q0q1 – занесём его в таблицу. Затем последовательно появятся q0q1q2, q0q3, q0q1q4. Все состояния исходного автомата, кроме q0, оказались недостижимыми. В таблице они выделены синим цветом. Удалим их.

состояние  a  b  c 
q0  {q0,q1}  {q0} {q0} 
q1  {q2}  –  – 
q2  –  {q3}  – 
q3  {q4}  –  – 
q4  –  –  – 
q0q1 A {q0q1q2} {q0} {q0} 
q0q1q2 B {q0q1q2} {q0q3} {q0} 
q0q3 C {q0q1q4} {q0} {q0} 
q0q1q4 D {q0q1q2} {q0} {q0} 
 вход Новые состояния для удобства переобозначим A, B, C, D. Заключительными состояниями станут те, которые содержат q4. Здесь такое состояние одно – D. Новая таблица переходов представлена слева:

состояние  a  b  c 
q0  {A}  {q0}  {q0} 
A  {B}  {q0}  {q0} 
B  {B}  {C}  {q0} 
C  {D}  {q0}  {q0} 
D  {B}  {q0}  {q0} 

Граф переходов построен по таблице:
Q={q0,A,B,С,D }, F={D}.
ДКА построен.


Комментарии: Работа была зачтена с первого раза в 2014г.
Преподаватель: Бах О.А.

Размер файла: 411,4 Кбайт
Фаил: (.zip)
-------------------
Обратите внимание, что преподаватели часто переставляют варианты и меняют исходные данные!
Если вы хотите, чтобы работа точно соответствовала, смотрите исходные данные. Если их нет, обратитесь к продавцу или к нам в тех. поддержку.
Имейте ввиду, что согласно гарантии возврата средств, мы не возвращаем деньги если вариант окажется не тот.
-------------------

Скачать

Добавить в корзину

Занесено в корзину

    Скачано: 15         Коментариев: 0

Есть вопросы? Посмотри часто задаваемые вопросы и ответы на них.
Опять не то? Мы можем помочь сделать!

Некоторые похожие работы:

Курсовая работа по дисциплине: Теория языков программирования и методы трансляции. Вариант 08 (18, 28 и т.д.)
Курсовая работа по дисциплине: Теория языков программирования и методы трансляции. Вариант №8(18) 2022 г.
Ещё искать по базе с такими же ключевыми словами.