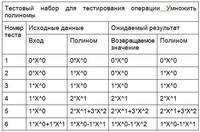
320

Современные технологии программирования. Лабораторная работа №7. Вариант: 8

ID: 149952
Дата закачки: 01 Февраля 2015
Продавец: Shamrock (Напишите, если есть вопросы)
    Посмотреть другие работы этого продавца

Тип работы: Работа Лабораторная
Форматы файлов: Microsoft Word, Pascal
Сдано в учебном заведении: СибГУТИ

Описание:
Лабораторная работа. Абстрактный тип данных (ADT) «полином»
Тема: Классы Object Pascal, стандартный класс Tlist.
Цель: Сформировать практические навыки: реализации абстрактных типов данных с помощью классов Object Pascal.
Задание
1. Реализовать тип «полином», в соответствии с приведенной ниже спецификацией.
2. Оттестировать каждую операцию, определенную на типе данных одним из методов тестирования.
3. Оттестировать тип данных в целом.
Спецификация абстрактного типа данных Полином.
ADT TPoly

Данные
Полиномы Tpoly - это неизменяемые полиномы с целыми коэффициентами.

Операции
Операции могут вызываться только объектом «полином» (тип TPoly), указатель на который передаётся в них по умолчанию. При описании операций этот объект в разделе «Вход» не указывается.
Описание операций на ADT TPoly.
Конструктор
Начальные значения: Коэффициент (с) и степень (n) одночленного полинома
Процесс:
Создаёт одночленный полином с коэффициентом (с) и степенью (n), или ноль-полином, если коэффициент (с) равен 0 и возвращает указатель на него.
Например:
Конструктор(6,3) = 6x^3
Конструктор(3,0) = 3
Конструктор() = 0
Выход: Указатель на созданный полином.
Постусловия: Нет.

Степень:
Вход: Нет.
Предусловия: Нет.
Процесс: Отыскивает степень n полинома, т.е. наибольшую степень при ненулевом коэффициенте (c). Степень нулевого полинома равна 0.
Например:
a = (x^2+1), a.Степень = 2
a = (17), a. Степень = 0
Выход: n - целое число - степень полинома.
Постусловия: Нет.

Коэффициент
Вход: n - целое число - степень полинома.
Предусловия: Полином – не нулевой.
Процесс: Отыскивает коэффициент (c) при члене полинома со степенью n (c*x^n). Возвращает коэффициент (c) найденного члена или 0, если n больше степени полинома.
Например:
p = (x^3+2x+1), p.Coeff (4) = 0
p = (x^3+2x+1), p.Coeff (1) = 2
Выход: Целое число.
Постусловия: Нет.

Сложить
Вход: q - полином.
Предусловия: Нет
Процесс: Создаёт полином, являющийся результатом сложения полинома с полиномом q и возвращает его.
Выход: Полином.
Постусловия: Нет.

Умножить
Вход: q - полином.
Предусловия: Нет.
Процесс: Создаёт полином, являющийся результатом умножения полинома на полином q и возвращает его.
Выход: Полином.
Постусловия: Нет.

Вычесть
Вход: q - полином.
Предусловия: Нет.
Процесс: Создаёт полином, являющийся результатом вычитания из полинома полинома q и возвращает его.
Выход: Полином.
Постусловия: Нет.

Минус
Вход: Нет.
Предусловия: Нет.
Процесс: Создаёт полином, являющийся разностью ноль-полинома и полинома и возвращает его.
Выход: Полином.
Постусловия: Нет.

Равно
Вход: q - полином.
Предусловия: Нет.
Процесс: Сравнивает полином с полиномом q на равенство. Возвращает значение True, если полиномы равны, т.е. имеют одинаковые коэффициенты при соответствующих членах, и значение False - в противном случае.
Выход: Булевское значение.
Постусловия: Нет.

Дифференцировать
Вход: Нет.
Предусловия: Нет.
Процесс: Создаёт полином, являющийся производной полинома и возвращает его.
Например: a = (x^3+7x+5),
a.Дифференцировать = 3x^2+7
Выход: Полином.
Постусловия: Нет.

Вычислить:
Вход: x – действительное число.
Предусловия: Нет.
Процесс: Вычисляет значение полинома в точке x и возвращает его.
Например: a = (x^2+3x), а.Вычислить(2) = 10
Выход: Действительное число.
Постусловия: Нет.

Элемент
Вход: i - целое число - номер члена полинома.
Предусловия: Нет.
Процесс: Обеспечивает доступ к члену полинома с индексом i для чтения его коэффициента (c) и степени (n) так, что если изменять i от 0 до количества членов в полиноме минус один, то можно просмотреть все члены полинома.
Выход: Коэффициент – целое число, степень – целое число.
Постусловия: Полином не модифицируется

end Tpoly

Рекомендации к выполнению
1. Тип данных реализовать, используя классы Object Pascal.
2. Полином можно рассматривать как список одночленных полиномов, поэтому для реализации полинома полезно реализовать абстрактный вспомогательный тип данных одночленный полином. Спецификация для него приведена ниже.
Спецификация абстрактного типа данных Одночлен.
ADT TMember

Данные
Одночлен TMember - это изменяемые одночленные полиномы с целыми коэффициентами. Коэффициент и степень хранятся в полях целого типа FCoeff и FDegree соответственно.

Операции
Операции могут вызываться только объектом «одночлен» (тип TMember), указатель на который передаётся в них по умолчанию. При описании операций этот объект в разделе «Вход» не указывается.
Описание операций на ADT TMember.

Конструктор
Начальные значения: Коэффициент (с) и степень (n) одночленного полинома
Процесс: Создаёт одночленный полином с коэффициентом (с) и степенью (n), или ноль-полином, если коэффициент (с) равен 0 и возвращает указатель на него.
Например:
Конструктор(6,3 = 6x^3
Конструктор(3,0) = 3
Конструктор() = 0
Выход: Указатель на созданный одночленный полином.
Постусловия: Нет.

ЧитатьСтепень
Вход: Нет.
Предусловия: Нет.
Процесс: Возвращает степень n одночленного полинома (содержимое поля FDegree). Степень нулевого полинома равна 0.
Например:
a = (1x^2), a.Степень = 2
Выход: n - целое число - степень полинома.
Постусловия: Нет.

ПисатьСтепень
Вход: n - целое число - степень полинома.
Предусловия: Нет.
Процесс: Записывает степень n одночленного полинома в поле FDegree.
Выход: Нет.
Постусловия: Поле FDegree = n.

ПисатьКоэффициент
Вход: c - целое число - коэффициент полинома.
Предусловия: Нет.
Процесс: Записывает коэффициент c одночленного полинома в поле FCoeff.
Выход: Нет.
Постусловия: Поле FCoeff = c.

Равно
Вход: q - одночлен.
Предусловия: Нет.
Процесс: Сравнивает одночлен с одночленом q на равенство. Возвращает значение True, если одночлены равны, т.е. имеют одинаковые коэффициенты и степени, и значение False - в противном случае.
Выход: Булевское значение.
Постусловия: Нет.

Дифференцировать
Вход: Нет.
Предусловия: Нет.
Процесс: Создаёт одночлен, являющийся производной одночлена и возвращает его.
Например: a = (x^3),
a.Дифференцировать = 3x^2
Выход: Одночлен.
Постусловия: Нет.

Вычислить
Вход: x – действительное число.
Предусловия: Нет.
Процесс: Вычисляет значение одночлена в точке x и возвращает его.
Например: a = (1x^2), а.Вычислить(2) = 4
Выход: Действительное число.
Постусловия: Нет.

ОдночленВСтроку
Вход: Нет.
Предусловия: Нет.
Процесс: Формирует строковое представление одночлена.
Выход: Строка.
Постусловия: Нет.

end TMember

3. Для хранения членов полинома используйте список Tlist для этого класс Tpoly, реализующий тип данных полином, сделайте наследником от класса Tlist:
TPoly = class(TList)
private
function Get: String;virtual;
function GetMember(index: Cardinal): TMember;virtual;
procedure SetMember(index: Cardinal; E: TMember);virtual;
public
constructor Create(nc: Integer = 0; nd: Integer = 0);
destructor Destroy;override;
function Degree: cardinal;
function Coeff(n: Integer): Integer;
property Poly: String read Get;
function _Add(b: TPoly): TPoly;//Операция Сложить.
function Sub(b: TPoly): TPoly;// Операция Вычесть.
function Minus: TPoly;// Операция Минус.
function Mul(b: TPoly): TPoly;// Операция Умножить.
function Diff: TPoly;// Операция Дифференцировать.
function Eval(v: Real): Real;// Операция Вычислить.
function Eqval(b: TPoly): Boolean;// Операция Равно.
property Member[index: Cardinal]: TMember read GetMember;
//Операция Элемент.
private
procedure RemoveZero;//Удаляет члены с нулевыми //коэффициентами.
procedure Likeness;//Приведение подобных.
procedure Invar;//Преобразует полином к стандартному виду:
//упорядочен, приведены подобные, удалены нулевые //члены.
procedure AddCopies(b: TPoly; k: Integer);//добавляем копии //элементов b в хвост.
function MulNum(Num: TMember): TPoly;//Умножение //полинома на одночлен.
end;

4. Для реализации одночленного полинома (одночлена) создайте класс Tmember, в который вынесите все операции на членах полинома:
TMember = class
// Реализует одночлен вида FCoeff * X^ FDegree.
private
FDegree: Integer;//Степень одночлена.
FCoeff: Integer;//Коэффициент одночлена.
function Get: String;
//Операция ОдночленВСтроку.
function GetCoeff: Integer;
//Операция ЧитатьКоэффициент (поля FCoeff).
function GetDegree: Integer;
//Операция ЧитатьСтепень (поля FDegree).
procedure SetDegree(nd: Integer);
//Операция ПисатьСтепень (поля FDegree).
procedure SetCoeff(nc: Integer);
//Операция ПисатьКоэффициент (поля FCoeff).
public
function Diff: TMember;
//Операция Дифференцировать.Дифференцирование одночлена.
function Value(v: Real): Real;
//Операция Вычислить. Вычисляет значение одночлена.
property Coeff: Integer read GetCoeff write SetCoeff;
//Операция для чтения и записи коэффициента (поля FCoeff).
property Degree: Integer read GetDegree write SetDegree;
//Операция для чтения и записи степени (поля FDegree).
property Member: String read Get;
//Операция ОдночленВСтроку. Свойство для чтения одночлена в
//строковом формате.
function Eq(b: TMember): Boolean;
//Операция Равно. Сравнение одночлена с одночленом b.
constructor Create(nd: Integer = 0;nc: Integer = 0);
end;
5. После выполнения каждой операции приводите полином к нормализованному виду: упорядочить, привести подобные, удалить нулевые члены (члены с нулевыми коэффициентами).
6. Тип данных реализуйте в отдельном модуле UPoly.
Порядок выполнения
В режиме консольного приложения
• опишите класс TMember, реализуйте класс и оттестируйте каждый метод.
• опишите класс TPoly, реализуйте класс и оттестируйте каждый метод и класс в целом.
Тестовые наборы поместите в таблицу следующего вида (см.вложение)

Содержание отчета
1. Задание.
2. Текст программы на Object Pascal.
3. Тестовые наборы данных для тестирования типа данных.

Контрольные вопросы
1. Чем определяется размер памяти, выделяемой под экземпляр класса?
2. Что такое RTTI класса?
3. Как и когда происходит связывание объекта с RTTI класса?
4. Как описываются и переопределяются виртуальные и динамические методы?
5. Что такое раннее связывание, и для каких методов оно выполняется?
6. Что такое позднее связывание, и для каких методов оно выполняется?
7. Когда для класса необходимо описать собственный деструктор?




Комментарии: Работа была зачтена с первого раза в 2014г.
Преподаватель: Зайцев М.Г.

Размер файла: 120,7 Кбайт
Фаил: (.zip)
-------------------
Обратите внимание, что преподаватели часто переставляют варианты и меняют исходные данные!
Если вы хотите, чтобы работа точно соответствовала, смотрите исходные данные. Если их нет, обратитесь к продавцу или к нам в тех. поддержку.
Имейте ввиду, что согласно гарантии возврата средств, мы не возвращаем деньги если вариант окажется не тот.
-------------------

Скачать

Добавить в корзину

Занесено в корзину

    Скачано: 2         Коментариев: 0

Есть вопросы? Посмотри часто задаваемые вопросы и ответы на них.
Опять не то? Мы можем помочь сделать!

Некоторые похожие работы:

Современные технологии программирования. Лабораторная работа 1,2,3. Вариант 3
ЛАБОРАТОРНЫЕ РАБОТЫ №1-3 по дисциплине «Современные технологии программирования (часть 2)». Вариант общий. 2019 год.
Лабораторные работы №1,2,3 по дисциплине: Современные технологии программирования (часть 1). Для всех вариантов
Современные технологии программирования (часть 1). Лабораторные работы 1-3. Все варианты. 2019
Лабораторные работы №1,2,3 по дисциплине: Современные технологии программирования (часть 2). Для всех вариантов (Новое)
Современные технологии программирования (часть 2). Лабораторные работы 1-3. Все варианты. 2019
Лабораторные работы №№ 1-7 по дисциплине: "Современные технологии программирования". Вариант №5
Ещё искать по базе с такими же ключевыми словами.