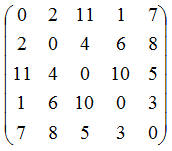Страницу Назад
Поискать другие аналоги этой работы
100 Теория сложностей, вычислительных процессов и структур. Экзамен. Билет №1. 2016гID: 165088Дата закачки: 08 Апреля 2016 Продавец: vasiakollaider (Напишите, если есть вопросы) Посмотреть другие работы этого продавца Тип работы: Работа Экзаменационная Форматы файлов: Microsoft Office Сдано в учебном заведении: СибГУТИ Описание: 1. По алгоритму Краскала найти остов минимального веса для связного взвешенного неориентированного графа, имеющего 5 вершин. Граф задан матрицей весов дуг, соединяющих всевозможные пары вершин 2. Оптимальным образом расставить скобки при перемножении матриц М1[7x3], M2[3x8], M3[8x3], М4[3x5], M5[5x2] Комментарии: Коментарии: Уважаемый слушатель, дистанционного обучения, Оценена Ваша работа по предмету: Теория сложностей вычислительных процессов и структур Вид работы: Экзамен Оценка:Отлично Дата оценки: 03.04.2016 Рецензия:Уважаемая поздравляю Вас с успешным завершением курса ТСВПиС. Галкина Марина Юрьевна Размер файла: 44 Кбайт Фаил:
Скачано: 4 Коментариев: 0 |
||||
Есть вопросы? Посмотри часто задаваемые вопросы и ответы на них. Опять не то? Мы можем помочь сделать! |
||||
Вход в аккаунт:
Страницу Назад
Cодержание / Теория сложностей вычисл. процессов и структур / Теория сложностей, вычислительных процессов и структур. Экзамен. Билет №1. 2016г
Вход в аккаунт: