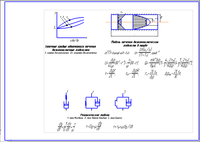
434

Чертежи-Графическая часть-Курсовая работа-Типичные кривые одномерного течения вязкопластичных жидкостей, Модель течения вязкопластической жидкости в трубе, Реологические модели, Совмещенная характеристика нефтепровода и насосных станций данного расчета,

ID: 166593
Дата закачки: 07 Мая 2016
Продавец: https://vk.com/aleksey.nakonechnyy27 (Напишите, если есть вопросы)
    Посмотреть другие работы этого продавца

Тип работы: Чертежи
Форматы файлов: КОМПАС
Сдано в учебном заведении: ИНиГ

Описание:
Реология (от греческого rheo - «течь») - это раздел физики, в ко¬тором рассматриваются вопросы деформации и текучести веществ. Это название было предложено в 1929 г. Бингамом (Е.С. Bingham). Ближе всего реология примыкает к механике или, точнее, к физико-химической механике.
Задачей реологии является установление взаимосвязи между силами, действующими на среду, и вызванными ими деформациями. Если при этом материя рассматривается так, как она представляется нашим ощущениям, т.е. как сплошная среда, то речь идет о феноменологической реологии. Феноменологические модели применяются при отсутствии сведений о деталях организации рассматриваемой системы. На этом уровне описания среда рассматривается как «черный ящик» и задача реологии сводится к проведению ключевых опытов, раскрывающих связь между входными (деформации) и выходными (напряжения) сигналами. Но внутренняя орга-низация исследуемой среды при этом остается скрытой. Концептуальная реология (или микрореология) выводит реологические соотношения теоре-тическим путем, опираясь на достижения физики и химии. В настоящее время наиболее развит структурно-кинетический подход, со¬гласно которому процессы разрушения и восстановления структурных связей в жидкости схематично представляются как прямая и обратная! химические реакции, суммарное действие которых описывается некото¬рым кинетическим уравнением относительно концентрации связей.
Концептуальный подход имеет преимущества в строгости и общно¬сти, однако обладает тем недостатком, что может разрешить только огра-ниченный круг проблем. Перефразируя известное замечание , можно сказать, что концептуальная реология решает те задачи, которые может так, как нужно, а феноменологическая реология решает те задачи, которые нужно так, как она может. Преимуществом феноменологического подхода является его высокая прагматическая нацеленность на решение инженерных задач; часто фено¬менологические модели способствуют обоснованию и мотивировке концептуальных моделей.
При описании реальных сред весьма полезными оказываются представления об идеальных телах, проявляющих простейшие реологические свойства: упругость, пластичность и вязкость. В качестве материальных носителей этих свойств можно представить себе соответственно сталь, пластилин и воду. Конечно, каждое вещество в реальности обладает всеми реологическими свойствами, хотя и в различной степени. Так, если сталь подвергнуть напряже¬нию порядка 108 Па, то она начинает проявлять пластические свойства. Поэтому реальные материалы представляются в виде некоторых комбина¬ций трех фундаментальных идеальных тел. В литературе идеальные тела принято называть именами ученых, которые ввели их впервые: упругое тело называется телом Гука (Нооке, 1635-1703 гг.), пластическое - телом Сен-Венана (St. Venant, 1797-1886 гг.), вязкое - телом Ньютона (I. Newton, 1642-1726 гг.).
Каждый материал характеризуется двумя реологическими уравне-ниями: одним для объемных деформаций (под действием всестороннего равномерного сжатия) и другим - для деформаций формоизменения (под последними чаще всего понимаются сдвиговые деформации). Классиче¬ская реология предполагает, что при всестороннем давлении все мате¬риалы (и твердые и жидкие) ведут себя как идеально упругие тела. Это предположение в большинстве случаев является весьма хорошим прибли-жением, но при объемном деформировании структурных жидкостей могут проявить себя объемная вязкость и релаксация, нарушающие его справед-ливость.
Наиболее ярко реологическое различие между сталью и пластилином проявляется при сдвиговых деформациях. Математически это различие в поведении при сдвиге можно выразить, рассматривая мысленно призмы, вырезанные из разных материалов .
1.1.1. Упругое тело
Прежде всего рассмотрим малую призму из стали, находящуюся под действием тангенциальной силы F, приложенной к верхней горизонталь¬ной грани (рис.1.1)Очевидно величина сдвига призмы определяется углом ,образованным вертикальными и скошенными боковыми гранями. Поскольку то в качестве меры сдвига можно использовать именно это отношение (здесь U- смещение верхней грани, Н -высота призмы). Путем перехода к бесконечно малым величинам величину сдвига можно определить как


Рисунок 1.1 Сдвиг элементарной призмы

За меру напряженности материала естественно принять касательную силу, приходящуюся на единицу площади верхней грани, т.е. отношение , называемое касательным напряжением. Предполагая, что напряжения пропорциональны деформациям, получим , где G называется модулем сдвига. Реальные значения этой величины меняются от 0,2-10 Па (свинец) до 8 • 1016 Па (сталь).
1.1.2. Пластическое тело
Если призма выполнена из пластилина, то при малых напряжениях ее поведение напоминает поведение стальной призмы, т.е. она тоже будет деформироваться упруго. Однако при достижении некоторого критиче-ского значения касательного напряжения Т, называемого пределом теку-чести при сдвиге, пластилин потечет. При этом напряжение будет оста-ваться приблизительно постоянным, а величина сдвига - безгранично расти. Реологическая модель пластического тела может быть записана в виде
Так, предел текучести металлов при сдвиге изменяется от 3-10 Па (алюминий) до 7,5 -107 Па (никель).


1.1.3. Вязкая деформация (течение)
Поскольку жидкую «призму» трудно себе представить, сдвиговую деформацию воды проиллюстрируем на примере знаменитого мысленного опыта Ньютона, рассмотревшего вязкую жидкость, заключенную между двумя бесконечно протяженными параллельными пластинами, нижняя из
которых неподвижна, а верхняя движется с некоторой скоростью v0
dU- смещение верхней пластины (рис 1.2)

Рисунок 1.2 Течение вязкой жидкости
Представим себе, что жидкость разделена на бесконечно тонкие горизонтальные плоские слои, которые при перемещении верхней пластины скользят один по другому так же, как карты в сдвигаемой колоде. Если скорость 0 бесконечно мала, то эта деформация не требует сколько-нибудь заметного усилия, хотя величина смещения U может расти безгранично.
Только тогда, когда скорость 0 будет конечна, возникает сила сопротивления, вызванная трением слоев жидкости относительно друг друга. Отсюда ясно, что мерой сдвиговых деформаций жидкости является
не величина , а аналогичное ей отношение , называемое
скоростью сдвига (Н-расстояние между пластинами). Поскольку то скорость сдвига часто обозначается символом (напомним, что в механике точка соответствует дифференци¬рованию по времени). Силы, необходимые для сдвига жидкости, по-преж¬нему определяются касательным напряжением F/S, где F - сила сопротивления, возникающая на площади S из-за затрудненного проскальзывания соседних слоев жидкости. Предполагая, что касательное напряжение пропорционально скорости сдвига (Ньютон, 1687 г.), получим , где величина называется вязкостью жидкости. Материалы, описываемые этим уравнением, называются ньютоновскими жидкостями. Реальные значения вязкости изменяются в очень широких пределах. Так, при 20°С вода имеет вязкость Па с, а глицерин - 1,5 Па с.
На рис. 1.3 приведены реологические кривые - \'зависимости касатель¬ного напряжения от меры сдвига - для трех рассмотренных выше материалов

Рисунок 1.3 Реологические кривые
а) упругое тело; б) пластическое тело; в) вязкая жидкость.
Такие диаграммы могли бы быть получены в ходе экспериментов с идеальными телами при постепенном увеличении напряжения (нагрузке) и обратном его уменьшении (разгрузке). Стрелки на приведенных диаграм-мах указывают направление, в котором изменяется напряжение.
Реологическая диаграмма пластического тела имеет упругий участок вплоть до предела текучести. При снятии напряжений эта часть полной деформации обратима, а те деформации, что были накоплены в процессе течения, являются необратимыми (см. рис. 1.3, б). Хорошо всем знакомым примером такого тела является зубная паста [191]. Если слегка сдавить тюбик с зубной пастой, то плоская поверхность пасты в выходном отвер-стии становится выпуклой, но при снятии давления эта выпуклость исче-зает. Если же тюбик сжимается с большей силой, то происходит необрати-мое выдавливание цилиндрика пасты. Присмотревшись, можно заметить, что на конце этого цилиндрика образуется сферический сегмент, пропа-дающий после снятия нагрузки за счет исчезновения обратимых нагрузок.


Размер файла: 135,1 Кбайт
Фаил: (.rar)

Скачать

Добавить в корзину

Занесено в корзину

        Коментариев: 0

Есть вопросы? Посмотри часто задаваемые вопросы и ответы на них.
Опять не то? Мы можем помочь сделать!

Некоторые похожие работы:

К сожалению, точных предложений нет. Рекомендуем воспользоваться поиском по базе.